Table of Contents
Geometry
Geometry: Geometry is the oldest branch of mathematics which deals with the size, shapes, position angles, and dimensions of things. Geometry deals with the things which are used in daily life. Geometry includes 2D as well as 3D shapes i.e 2 dimensional and 3-dimensional shapes.
In-plane geometry, 2d shapes such as triangles, squares, rectangles, and circles are also called flat shapes. In solid geometry, 3d shapes such as a cube, cuboid, cone, etc. are also called solids. The basic geometry is based on points, lines, and planes which come under coordinate geometry.
In this article, we are providing you the detailed information about geometry, geometry shapes, and geometry formulas. Understanding geometry will help candidates to solve the problems related to that and asked in the competitive exams.
Geometry Definition
Geometry word is derived from Ancient Greek words – ‘Geo’ means ‘Earth’ and ‘metron’ means ‘measurement’. Geometry is concerned with properties of space that are related to distance, shape, size, and relative position of figures. The basics of geometry depend on majorly points, lines, angles, and planes.
What are the Branches of Geometry?
The branches of geometry are as follows:
- Algebraic geometry
- Discrete geometry
- Differential geometry
- Euclidean geometry
- Convex geometry
- Topology
Plane Geometry (2D Geometry)
Plane Geometry means flat shapes which can be drawn on a piece of paper. These include lines, circles & triangles of two dimensions. Plane geometry is also known as a two-dimensional geometry. Example of 2D Geometry is square, triangle, rectangle, circle, lines, etc. Here we are providing you with the properties of the 2D shapes below.
Point
A point is a location or place on a plane. A dot usually represents them. It is important to understand that a point is not a thing, but a place. The point has no dimension and it has the only position.
Line
The line is straight with no curves), has no thickness, and extends in both directions without end infinitely.
Angles in Geometry
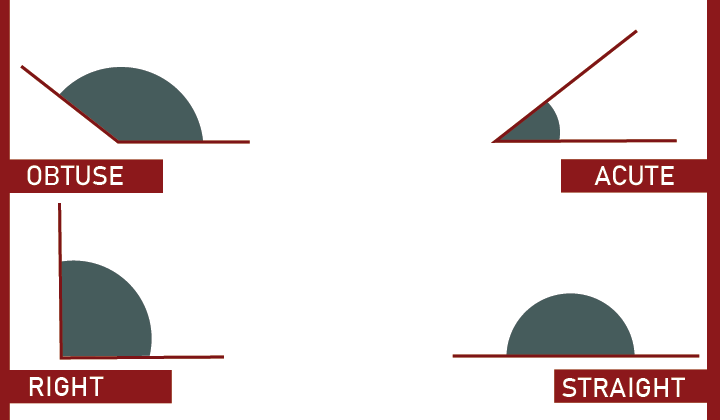
Angles are formed by the intersection of two lines called rays at the same point. which is called the vertex of the angle.
Types of Angle
- Acute Angle – An Acute angle is an angle smaller than a right angle ie. it can be from 0 – 90 degrees.
- Obtuse Angle – An Obtuse angle is more than 90 degrees but is less than 180 degrees.
- Right Angle – An angle of 90 degrees.
- Straight Angle – An angle of 180 degrees is a straight angle, i.e. the angle formed by a straight line
Polygons
Types of Polygons
The types of polygons are:
- Triangles
- Quadrilaterals
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Nonagon
- Decagon
We have discussed the property as well as examples of the polygons with their properties in the below table. These figures will help candidates prepare for geometry for various competitive exams.
| Triangle | A 3-sided polygon whose sum of internal angles always sums to 180 degrees. |
|
| Quadrilateral | A 4-sided polygon with four edges and four vertices with a sum of internal angles is 360 degrees |
|
| Pentagon | A plane figure with five straight sides and five angles | – |
| Hexagon | A plane figure with six straight sides and six angles | – |
| Heptagon | A plane figure with seven sides and seven angles | – |
| Octagon | A plane figure with eight straight sides and eight angles. | – |
| Nonagon | A plane figure with nine straight sides and nine angles. | – |
| Decagon | A plane figure with ten straight sides and ten angles. | – |
Geometry Formulas
Every geometry shape and figure has its own formula for the area and perimeter. This is important for the candidates to solve various questions asked in the geometry section in the Quantitative Aptitude section of Competitive exams. All the important Geometry formulas are tabulated below.
| Shape | Area | Perimeter |
| Rectangle (l= Length and b= breadth) | (l*b) | 2(l+b) |
| Square (a is the side of the square) | a2 | 4a |
| Triangle (a,b and c are sides of the triangle) | 1/2 (b × h) | a + b +c |
| Circle (r = radius) | πr2 | 2πr (Circumference of Circle) |
| Parallelogram (a = side, b=base ,h=vertical height) | A = b × h | P = 2(a+b) |
Geometry Shapes and Formulas: FAQ
Q. What is the area of Triangle?
Ans: The area of a triangle is 1/2( b × h).
Q. What are the types of angles?
Ans: These are 4 types of angles ,i.e. acute, obtuse, right, and straight angle.
Q. What is Geometry?
Ans: Geometry is a branch of mathematics that deals with shapes, angles, dimensions, and sizes.
