Percentage is a way of expressing a number as a part of 100. It is denoted by the symbol “%“. Percentages indeed serve as a valuable tool for expressing relative quantities and making comparisons, and they find application in a wide range of fields, including finance, economics, education, and competitive examinations.
In competitive examinations, the knowledge of percentages can be utilized to solve questions from different topics. Some of the direct applications of percentage can be seen in Average, Profit & Loss, Simple & Compound Interest, Time & Distance, Time & Work, Simplification, etc. It can also play an important role in questions asked in Mensuration, Geometry, and Trigonometry.
Percentage Calculation
In this article, we are providing the basic definition of a percentage along with the formula of percentage and percentage questions which helps you with a percentage calculation and increase your score in the government competitive exams. You can learn shortcut percentage methods, and formulas to solve the questions on this topic. To score good marks in any exam, it is necessary to have knowledge of the important topics and clear the basic concepts.
Percentage Definition
Percentage is a mathematical expression used to represent a fraction of a whole, usually denoted by the symbol “%.” It is a way of expressing a part or a portion of something in relation to the whole, typically out of 100. In other words, it quantifies how much one quantity or value represents concerning the total or the entire quantity.
The formula to calculate the percentage of a quantity in relation to the whole is:
Percentage = (Part/ Whole) × 100
Here’s what each component represents:
- Percentage: The result you’re trying to find, represented as a percentage value.
- Part: The specific quantity or portion you’re interested in.
- Whole: The total or the entire quantity.
How to Calculate Percentage?
Here we are providing some examples to give you samples of how to calculate percentages using the percentage formula. These questions will help you to understand the Percentage, and percentage formula using a percentage calculator.
Percentage Sample Questions
Example 1: There are 200 students in a class. Out of them, 90 are girls. Find the percentage of girls in the class.
Solution: We are given,
Total students in the class=200
Girls in the class = 90
Percentage of girls in the class = (Girls in the class⁄ Total no. of students) × 100
Percentage of girls in the class = (90/200)x100 = 45%
Example 2: The price of a $1.50 candy bar is increased by 25%. Calculate the new price.
Solution: We are given,
Price of the Candy= $1.50
Increase in the price of candy= 25% or 25/100
New Price of candy= Old Price + increase in price
New Price of candy= 1.50 +25/100
New Price of candy= 1.50 + 1.50 ×.25
New Price of candy= $ 1.875
Example 3: Radha earns a monthly salary of $1200. She spends $280/month on food. What percent of the monthly salary does she save?
Solution: Monthly salary of Radha= $1200
Salary saved by Radha = $(1200 – 280) = $920
The fraction of salary she saves = 920/1200
Percentage of salary she saves = (920/1200)×100 = 920/12 = 76.667 %
Example 4: There are two numbers. If the first number is 20% larger than the second number then by how much percentage is the second number smaller than the first number?
Solution: Let us assume that the numbers stated here are x and y respectively.
Let the value of y be 100. So, the first number that is 20% larger than y will be 120.
x = 120, y = 100
Now as asked in the question, the second number is 20 less than the first number. To arrive at the answer, we have to convert this into percentage.
Therefore, the required answer is = (20/120) X 100% = (100/6)% = 16.667%
Example 5: What is the cosine of 1/6th of a circle?
Solution: As we know, a circle represents 360 degrees and 1/6th of a circle will be 60 degrees.
In the question, we have been asked to find the cosine (or cos) of 60 degrees.
Hence the required answer is = Cos(60o) = 1/2 = 0.50
Example 6: A rectangular plot of land with length 10 meters and breadth 20 meters is to be fenced. As of now only 40 % of the fencing has been completed find the length of the fence that is left to be laid around the plot.
Solution: Length of the plot = 10 meters Breadth of the plot = 20 meters.
So, the perimeter of the plot of land = 2 X (Length + Breadth) = 2 X (10 + 20) = 60 meters
Now, we have to calculate the remaining length of the perimeter that is to be faced i.e. (100-40)% = 60% of the fence.
The required answer is = 60% of 60 meters = 36 meters
Percentage Chart
A candidate who has the knowledge of common fractions and their values in percentage has a clear advantage over the competition as it can save him/her lots of time spent in lengthy calculations. The table below lists out some common fractions and their corresponding percentages.
| Fraction | Percentage |
|---|---|
| 1/2 | 50.00% |
| 1/3 | 33.33% |
| 1/4 | 25.00% |
| 1/5 | 20.00% |
| 1/6 | 16.66% |
| 1/7 | 14.28% |
| 1/8 | 12.50% |
| 1/9 | 11.11% |
| 1/10 | 10.00% |
Percentage Notes
In competitive examinations such as the SSC and Railway exams, the concept of percentages is very useful in questions of different topics in the quantitative aptitude section of the paper. The candidates preparing for these exams should prepare their handwritten notes on the various aspects of the concepts of percentages. The points provided below are examples of how to make notes for this topic.
- If the question states that A is 50% as efficient as B. It means that if B can do a piece of work in 1 day, then A will do the same work in 2 days.
- The relation between the volume of a cylinder and that of a cone of the same radius and height can be expressed in terms of ratio and percentage, e,g, Volume of Cone: Volume of Cylinder = 1:3. This also means that the volume of the cone will be 33.33% of that of the cylinder.
- One of the most important applications of percentages can be seen in the questions of simplification. The part of the equation that contains a term of percentage can be also interchanged with fractions for quick calculation.
- An important point to keep in mind while making notes on percentages is that while solving questions in the exams, the candidates should use either percentage or ratio or fraction whichever provides the quickest and simplest solution.

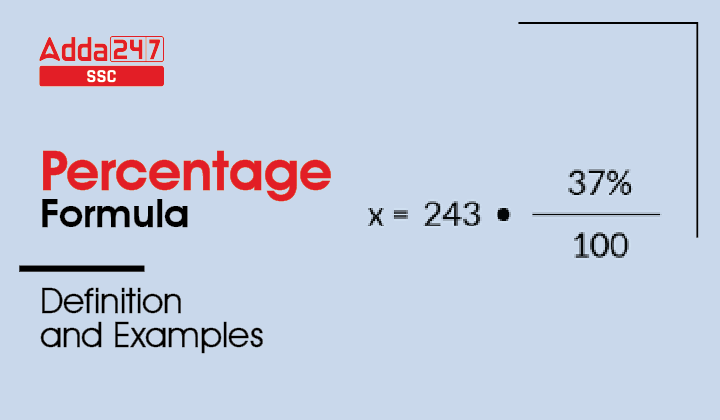


 Upcoming Government Exams, Complete Govt...
Upcoming Government Exams, Complete Govt...
 SSC Exam Calendar 2025–26 Out, Check All...
SSC Exam Calendar 2025–26 Out, Check All...
 RRB JE 2024 Notification, CBT 2 Exam Dat...
RRB JE 2024 Notification, CBT 2 Exam Dat...


